“Binary Search Trees in Java” is one of the most fundamental data structures. They organize data in a way that allows fast searching, insertion, and deletion operations, making them essential for efficient programming.
Understanding BSTs is crucial for solving real-world problems and implementing advanced algorithms. In this article, we will explore the structure, properties, and key operations of Binary Search Trees.
TL;DR: Binary Search Tree In Java
Aspect | Summary |
BST Definition | A Binary Search Tree (BST) is a binary tree where the left child is smaller and the right child is larger. This property applies recursively to all nodes. |
Core Operations | Insert, search, and delete are the main BST operations. Proper understanding prevents common mistakes and keeps the tree structured. |
Traversals | In-order traversal of a BST produces a sorted sequence. Preorder and postorder help in building and processing the tree efficiently. |
Complexity | Average case for operations is O(log n) in balanced trees, but the worst case can degrade to O(n) if the tree becomes skewed. |
Common Student Mistakes | Forgetting recursive returns, mishandling deletion cases, confusing traversal with search, and duplicate handling issues are frequent pitfalls. |
What Is Binary Search Tree In Java Programming Language?
You might already know about the “Tree concept” present in the Data Structures. The Tree concept is categorized under the Non-Linear Category.
In the Tree concept, there are many variations present. The Binary Search Tree is one such variation. Here, the concept is developed around the two-node root, which is popularly known as the Parent Node and Child Node or Leaf Node.
The Parent Node, Child Node, or Leaf Node can be divided further into three categories. These are the following:
Root Node: The Root Node is the main node of any Binary Search Tree. The main Root Node is the highest number of any root node present in the Binary Tree.
Left Child or Left Leaf Node: The node that is present at the left-hand side of any root node will be considered as the Left Child or Left Leaf Node. In the Binary Tree, the Left Child should always be smaller than the Main Root Node. It is the representative of the Left Subtree.
Right Child or Right Leaf Node: The Right Child is the main representative of the Right Subtree that is present below the Right Child. In the case of the Binary Tree concept, the Right Child will always be greater in number than the main Root Node.
Why Students Get Stuck In Java Binary Search Tree Programming Tasks?
A binary search tree (BST) is one of those topics that looks simple in theory but becomes confusing when students try to implement it in Java.
Based on common classroom doubts, exam answers, and coding mistakes, here’s why students usually struggle with BST:
1) Students Confuse A Binary Tree With a Binary Search Tree:
Many students think that if a node has a left and right child, it automatically becomes a Binary Search Tree. The real confusion comes from not understanding that a BST is defined by strict ordering rules, not just structure.
class Node {
int data;
Node left, right;
Node(int value) {
data = value; // value stored in node
}
}
Here, the code only creates a binary tree node, not a BST by itself. Without enforcing the BST logic ‘left < root < right’, students mistakenly assume the tree follows BST rules.
2) Recursion In BST Operations Feels Invisible:
BST insert and search operations rely heavily on recursion. Students often struggle because they cannot visualize how the function keeps calling itself and moves deeper into the tree.
void insert(Node root, int value) {
if (value < root.data)
root.left = new Node(value); // goes to left subtree
else
root.right = new Node(value); // goes to right subtree
}
Here, students miss that a real BST insert must repeat this logic recursively. Because recursion is not explicit, they think insertion happens in one step.
3) Traversal Output Is Mistaken For Tree Structure:
When students see that inorder traversal prints values in sorted order, they assume the BST stores data in sorted form internally, which is incorrect.
void inorder(Node root) {
if (root == null)
return;
inorder(root.left); // visit left subtree
System.out.print(root.data + " "); // visit node
}
The sorted output comes from the traversal logic, not the memory layout. This misunderstanding causes students to confuse data order with tree shape.
Explanation Of Java Binary Search Tree Properties:
From our expertise, we have seen that, in exams and viva voce, Binary Search Tree questions are usually scored based on clarity and correctness, not on lengthy explanations.
That is the reason understanding Binary Search Tree properties becomes very important. Here is the property explanation like an exam answer.
- For every node in the tree, all values in the left subtree are smaller than the node’s value, and all values in the right subtree are greater.
- This rule is not checked only at the root, but recursively at every node in the tree.
- If even one node violates this rule, the tree is no longer considered a BST, even if it looks balanced.
Exam Tip: Always mention the words “recursively applied property” in theory answers. It shows the conceptual clarity of a student.
What Is Binary Search Tree Java Implementation Process?
Here, the concept is based on creating a Node Container that will contain three types of information. One is Data, and the other two are the addresses of two children.
Program To Define The Process To Implement or Insert Elements Into The BST Using Java:
class BinaryST_Java {
class Node { // Class Node For Creating Node Structure
int key; // Taking Int Data From The Users
Node left, right;
public Node(int info){ // We will Not Create Private Node Root
key = info; // Inserting Int Data
left = right = null;
}
}
Node root; // Creating Root Node
BinaryST_Java(){ // Constructor For Binary Search Tree
root = null;
}
void insert(int key){ // Function To Insert A Node To BST
root = inRecur(root, key); // Creating New Node
}
Node inRecur(Node root, int key){ // Function To Recursively Insert Element
if (root == null){ // Condition To Check Empty Tree To Return Null
root = new Node(key); // Inserting Int Data To Node
return root; // We Will Return Root Here
}
if (key < root.key) // Inserting Element In The Left
root.left = inRecur(root.left, key); // Making Left Subtree
else if (key > root.key) // Inserting Element In The Right
root.right = inRecur(root.right, key);
return root; // We Will Return Root To Pointer
}
void print(){ // Function To Print The BST
Recurprint(root);
}
void Recurprint(Node root){ // Recuersive Print Function To Reduce Time Complexity
if (root != null) { // Checking Root Status
Recurprint(root.left); // Performing Inorder Traversal
System.out.print(root.key + "->");
Recurprint(root.right);
}
}
}
public class Main{
public static void main(String[] args) {
BinaryST_Java tree = new BinaryST_Java(); // Making Binary Search Tree Object
// Inserting Elements Into The Tree
tree.insert(10);
tree.insert(5);
tree.insert(3);
tree.insert(2);
tree.insert(15);
System.out.println("The Created Binary Search Tree: ");
tree.print(); // Printing The Entire BST
}
}
Steps Of The Program:
At first, a class node will be created that will hold all the values of any node. In any one, there will be Int Data, Left, and Right variables with the Node form.
The creation of one constructor is necessary to point out the nodes and to interconnect each and every node in the program.
The function to hold and insert the new node into the code will be declared. The function will first check whether the Binary Search Tree is empty or not. If it is empty, it will create a new node first.
Now, after creating the node, it will check the data. If the data is less than the root element, then it will be placed in the left subtree.
Otherwise, the data will be placed at the right subtree. And this process goes on in a recursive manner.
A function will again be created to print the BST necessarily. That means the left subtree will be first printed. Then, the Main Root Node will be printed. And at last, the right subtree will be printed.
In the main function, some elements will be inserted with the help of the BST Object that has been created. Now, the print function will be used, that is developed with the help of the Inorder traversal process.
Output:
From the above output, we can see that the element that is placed at the very left-most side will be printed first. So, the traversal of the left subtree can be done well with this program. As we are getting the entire node sequence, the program is marked as a working one.
What Is The Theory For Deleting Elements Into A Binary Search Tree?
Here, we will make three kinds of scenarios that you might find while deleting any node from the BST. Let us look at those scenarios or cases one by one.
Case 1: Node With No Child
If you want to delete a node on which no children are present, that means, no other node is attached to the chosen node, then you should not be worried. You can delete the node from the BST and move on to other operations.
Case 2: Node With Only One Child
In case there is only one child added to the node that is going to be deleted, you can do one simple operation. You can add the child to the above root of the deleted node. In this way, the concept will not be violated, and the node will get deleted.
Case 3: Node With Two Children
Now, if you want to delete a node with two children, then you need to use. Make the Node Left as the root node of the subtree. And the right node is kept as it is. That means the Node Left will become the root node to keep the rule of the BST.
How To Do Binary Search Tree Java Delete Operation?
Deleting can only be possible if there is an element present. That is the reason we have to first insert an element into the code and then delete some of them.
Program To Demonstrate The Delete Operation On Binary Search Trees:
class BST_Java {
class Node { // Class For Creating Node Structure
int key; // Taking Int Value From Main Function
Node left, right;
public Node(int info){ // Creating Public Node For Access
key = info;
left = right = null;
}
}
Node root; // Creating Root Node
BST_Java(){ // Constructor For Binary Search Tree
root = null; // We Will Return Node Here
}
void insert(int key){ // Function To Insert A Node To BST
root = inRecur(root, key);
}
Node inRecur(Node root, int key){ // Function To Recursively Insert Element
if (root == null){ // Condition To Check Empty Tree
root = new Node(key);
return root; // We Will Return Node Root
}
if (key < root.key) // Inserting Element In The Left
root.left = inRecur(root.left, key);
else if (key > root.key) // Inserting Element In The Right
root.right = inRecur(root.right, key);
return root; // Returning The Pointer
}
void del(int key) { // Function To Delete A Node
root = delr(root, key); // Accessing Public Node
}
Node delr(Node root, int key){ // Recusive Deleting Function
if (root == null) // If The Tree Is Empty
return root;
if (key < root.key)
root.left = delr(root.left, key); // Deleting From Left Tree
else if (key > root.key)
root.right = delr(root.right, key); // Deleting From Right Tree
else { // Condition For Nodes With One Child
if (root.left == null)
return root.right;
else if (root.right == null)
return root.left;
}
return root;
}
void print(){ // Function To Print The BST
Recurprint(root); // Performing Inorder Traversal
}
void Recurprint(Node root){ // Recuersive Print Function To Reduce Time Complexity
if (root != null) { // Checking Root Status
Recurprint(root.left);
System.out.print(root.key + "->");
Recurprint(root.right);
}
}
}
public class Main{
public static void main(String[] args) {
BST_Java tree = new BST_Java(); // Making Binary Search Tree Object
// Inserting Elements Into The Tree
tree.insert(10);
tree.insert(5);
tree.insert(3);
tree.insert(15);
System.out.print("The Created Binary Search Tree: ");
tree.print(); // Printing The Entire BST
System.out.println();
System.out.print("The New BST After Deletion: ");
tree.del(5); // Deleting The Element
tree.print(); // Printing The Entire Tree After Deletion
}
}
Steps Of The Program:
At first, we will follow the steps to create & insert elements into the BST, those are discussed earlier.
No,w for the delete operation, a function will be created. In this function, we will recursively check the presence of the element. If it is less than the Root, it will be on the Left Side. Otherwise, the node will be on the Right Subtree.
When we get the Node that should be deleted, it will be marked as Null so it will not be considered for printing purposes.
Now, in the main function, we will first print the entire BST. After the deletion operation, the printing operation will again be performed to see the changes.
Output:
From the above output, we can see that the BST design was done completely well, and the printing of the Binary Search Tree was completed without any errors. Now, we have deleted an element from the tree, and when we are again printing the tree, the element is not present.
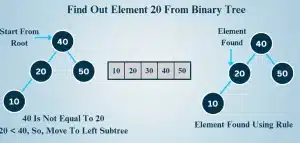
What Is The Theory For Searching Elements Into A Binary Search Tree?
Another important operation that can be done with the Binary Search Tree is the Searching operation. From the list of numbers that are present in the nodes, a particular number needs to be extracted.
And if the number is present in the list, it will be marked. To find out any element from the list, the following rules should be executed repeatedly. Here is the list of steps:
If the required number is less than the root number, go to the left subtree and find out.
If the required number is greater than the root number, go to the right subtree and find out.
We can go through the following image to clear the concept a bit more. In this case, a certain number needs to be found out with the help of the above-mentioned steps.
If you’re interested in discovering the Binary Search Tree concept for other programming languages like C++, then you can have a look at our article on BST in C++.
How To Implement The Code For Searching An Element Into Binary Search Tree?
In this case, we also, we need to first design the BST to find out a certain node number from the tree. So, the code for creating the Binary Search Tree will be used along with a new code snippet used for searching for the node number.
Java Code To Find Out Any Specific Number From The Given Binary Search Tree:
class BST_Java {
class Node { // Class Node For Creating Node Structure
int key;
Node left, right;
public Node(int info){
key = info;
left = right = null;
}
}
Node root; // Creating Root Node
BST_Java(){ // Constructor For Binary Search Tree
root = null;
}
void insert(int key){ // Function To Insert A Node To BST
root = inRecur(root, key);
}
Node inRecur(Node root, int key){ // Function To Recursively Insert Element
if (root == null){ // Condition To Check Empty Tree
root = new Node(key);
return root;
}
if (key < root.key) // Inserting Element In The Left
root.left = inRecur(root.left, key);
else if (key > root.key) // Inserting Element In The Right
root.right = inRecur(root.right, key);
return root; // Returning The Pointer
}
String searchkey(int key){ // Search Function That Returns String Value
root = sear(root, key);
if (root!= null) // If Node Is Present
return "Yes";
else // If Node Is Not Present
return "No";
}
Node sear(Node root, int key){
if (root==null || root.key==key)
return root;
if (root.key > key)
return sear(root.left, key);
return sear(root.right, key);
}
void print(){ // Function To Print The BST
Recurprint(root);
}
void Recurprint(Node root){ // Recuersive Print Function To Reduce Time Complexity
if (root != null) { // Checking Root Status
Recurprint(root.left);
System.out.print(root.key + "->");
Recurprint(root.right);
}
}
}
public class Main{
public static void main(String[] args) {
BST_Java tree = new BST_Java(); // Making Binary Search Tree Object
// Inserting Elements Into The Tree
tree.insert(10);
tree.insert(5);
tree.insert(3);
tree.insert(15);
System.out.print("The Created Binary Search Tree: ");
tree.print(); // Printing The Entire BST
System.out.println();
String result = tree.searchkey(150); // Searching For The Key
System.out.println("Is The Key 150 Found In BST? : " + result); // Checking The Key
}
}
Steps Of The Program:
Follow the steps that are used to design a BST using the Java program by inserting elements.
Declare the function to check the presence of any element. The class will use the searching rule and find out the element and its root number.
If the element is giving the root number, then the element is present. So, the String Value “YES” will be shared. Otherwise, the String Value “NO” will get shared.
Output:
From the above screenshot, we can see that the elements of the BST are printing successfully. Now, we are checking the presence of any element in the BST. As the element is not present in the BST, it will provide the NO value to the output.
Time And Space Complexity Of Binary Search Tree In Java:
When evaluating the performance of a Binary Search Tree in Java, we measure efficiency through the lens of Time Complexity and Space Complexity.
Understanding these complexities helps students avoid wrong assumptions in exams.
Time Complexity:
- Best and Average Case: For Search, Insert, and Delete, it is O(log n) when the tree is balanced.
- Worst Case: For Search, Insert, and Delete, it is O(n) when the tree becomes skewed, like a linked list.
Space Complexity:
- Space complexity mainly depends on the recursion depth.
- In the worst case, recursive calls can go up to the height of the tree (O(h)).
- For a skewed tree, space complexity becomes O(n) due to call stack usage.
Mental Model: How Students Should Think About A BST?
Oftentimes, we have seen students try to memorize the logic behind a Binary Search Tree. But this approach is heavily impacted during exams due to panic and exam pressure.
Instead of memorizing definitions, students should think of BST as a decision-making path. Here is a simple mental model that will help you a lot.
- Start from the root node.
- Compare the value you want to insert or search.
- If the value is smaller, move to the left child.
- If the value is greater, move to the right child.
- Repeat this process until you reach a null position or find the value.
This step-by-step comparison is the reason BST is faster than linear data structures when the tree is balanced.
How Many Binary Search Trees With n Nodes Can Be Possible?
It is a very important and tricky question that you can be asked by your university faculty or even during your interview related to Data Structure. Here, the number of nodes will be given to you. And the question will be asked, how many unique BSTs can be drawn with that number of nodes?
For that, you need to use the formula: Cn = (2n)! / ((n + 1)! * n!) Where n = 0, 1, 2, 3, …
If we consider the number of ‘n’ as 0, 1, 2, 3,…, the values of the potential number of Unique BST can be 1, 1, 2, 5, 14, 42, 132, 429, … and so on. So, remember this trick to calculate or provide an answer during your interview or viva.
Why Inorder Traversal Gives Sorted Output In Java BST?
Another important question that often comes in programming tasks and lab viva is on the Sorted Output of Inorder Traversal. In such cases, you have to write the answer like the following.
In a Binary Search Tree (BST), the reason Inorder traversal always produces a sorted output is not accidental; it is a direct result of how a BST is structured and how Inorder traversal works together with that structure.
A BST follows one simple rule:
- All values in the left subtree are smaller than the node
- All values in the right subtree are greater than the node
In-order traversal visits nodes in this order: First the left, then the root, and in the end the right.
So when we traverse the left subtree, we first get all the smaller values. Then we visit the root, and after that we traverse the right subtree, which contains only larger values.
Because this process is applied recursively at every node, the values are visited from the smallest to the largest.
That’s why Inorder traversal of a Binary Search Tree always produces a sorted sequence, without using any extra sorting logic in Java.
What Are Some Real-World Use Cases Of Binary Search Trees?
Binary Search Trees are widely used in Java programming because they allow efficient searching, insertion, and deletion of data.
Their structured way of organizing data makes them ideal for many real-world applications. Here are some common examples:
- BSTs are used in Java to build data structures like dictionaries or phone books, where quick lookup of names or numbers is essential.
- Applications like task schedulers or leaderboards use BSTs to keep data sorted while supporting frequent insertions and deletions.
- BSTs can store large vocabularies, enabling fast suggestions or corrections when users type words in search engines or text editors.
- File systems, organizational charts, and folder structures can be represented as BSTs to allow efficient navigation and updates.
- BSTs serve as the backbone for certain types of database indexing in Java, enabling quick retrieval of records based on key values.
Conclusion:
As we saw, the “Binary Tree Implementation and Several Operations” are really important to know.
Practice the code and the BST concept as much as possible to have a good grip on the Data Structures and Algorithm concepts. Try to define the Binary Search Tree code in other programming languages as well to excel in your skills.
It is always advisable to clear the basic programming concepts before tackling such an important and challenging topic in Java. If your foundation in the theory of BST and Java is rock-hard, then such a topic will become a walk in the park for you.
Key Takeaways:
- A BST stores data so that the left children are smaller and the right children are larger than the parent.
- In-order traversal of a BST naturally gives a sorted sequence of values.
- Searching, insertion, and deletion are fast when the tree is balanced.
- Handling duplicates carefully is important to maintain the BST property.
- BSTs are widely used in searching, sorting, and range-based queries in Java.
Frequently Asked Questions:
1) Why is BST efficient for search operations?
BSTs are efficient because they allow divide-and-conquer searching. At each node, you can decide to move left or right based on the value you are looking for.
2) What is the difference between a BST and a binary tree?
A regular binary tree has no ordering constraints on its nodes. In a BST, the left child is always smaller, and the right child is always larger than the parent. This ordering makes BSTs especially useful for searching, sorting, and range queries.
3) Can a Binary Search Tree become inefficient, and why?
Yes. A BST can degrade into a structure similar to a linked list if nodes are inserted in sorted or nearly sorted order. In such cases, the height of the tree becomes linear instead of logarithmic, making search, insertion, and deletion operations take O(n) time instead of O(log n).