Do you know how to build Max Heap with C programming language? Let’s experience the method to build Max Heap with C language.
Being the most popular programming language in the world, C programming is learned by students across the globe. It has many versatile concepts where students get stuck due to a lack of understanding of the subject knowledge and they look for C Programming help. So, today we are going to discuss a very common question asked by students on the Internet. Welcome to CodingZap’s new blog “How to build max heap from an array using C”.
Let us first discuss the Heap and its properties then we will jump into building max heap from an array in C programming.
What Is Heap? Read Below
Heap is a type of Data Structure. It is under the non-linear Data Structure. As the data has been stored there in a non-linear manner. The Heap structure in the Data Structure is quite likely similar to the Tree structure.
With the Tree in Data Structure, in Heap also, there are Left Child, and Right Child are available. In Heap, the main node is called the Root as in Tree. The lowermost child of the Heap is called the Leaf. This means the topmost node is the Root & the lowermost node is called the Leaf.
In this implementation, I am using a binary tree for simplicity.
How to represent a binary tree as an array?
Lets take a look at the methods where we represnt a binary tree as an array below:
- Root is at index 0 in the array.
- Left child of i-th node is at (2*i + 1)th index.
- Right child of i-th node is at (2*i + 2)th index.
- The parent of the i-th node is at (i-1)/2 index.
What Are The Properties Of Heap?
A heap can be of two types based on either of two heap properties –
-
Max Heap
A max-heap is a heap in which the value of each node is greater than or equal to the values of its children.
That means the root node value will always be greater than the Child node Values. It is not similar to the Binary Tree Data Structure. As in Binary Tree Data Structure, the Root Node Value will be greater than the Value of the Left Child. But it should be less than the Right Child value.
But in the case of Max Heap, the Root Node Values of the Tree or Subtree should be greater than or equal to both of the Child Values. We will build the Max Heap visualization concept in a better way.
-
Min-Heap
A min-heap is a heap in which the value of each node is less than or equal to the values of its children
Here, the Root Node Values will be lower than the values of their Child Node. The Root may be of the entire tree or maybe a subtree. The Root Node value will be less than or equal to the value of the Child Node value.
When To Use Min Heap And Max Heap?
After getting the information about the Min Heap & Max Heap, you should also note the scenarios where the Min & Max Heap should be used. Remember that in Min Heap, the minimum number is present as the root & for Max Heap, the maximum number occurs as the root.
This concept is used to categorise a series of numbers. The Min Heap is used to get the minimum component present in the series of numbers. Whereas the Max Heap is used to filter the highest number present in any series.
What Is Heapify?
Heapify is the basic building block of the algorithm of creating a heap data structure from a binary tree.
Heapify is the process by which a Heap is transferred to the Max Heap or the Min Heap. We build Max Heap with C programming language with the help of the Heapify process. We can say that Heapify is the small functional unit to build Max Heap with C programming language.
Heapify goes through a top-down approach and makes every subtree satisfy the max heap starting from the given node.
For implementing Heapify, there are certain steps to be followed. The algorithm of Heapify is very simple. Let’s know the steps of the algorithm briefly.
Step 1:
We need to find out the non-last leaf node of the Heap. Non-last Leaf node means that it must be a Root Node of the Tree itself. Or maybe it can be a Root Node of the subtree. Suppose, there are three nodes in the Tree. So, the non-last Leaf Node of the tree will be the Root Node of the Tree.
To find the Non-Last Leaf Node of the Heap, we need to memorize the formula: (n/2)-1 [Where n is the number of total nodes]
Here, in this case, the Root Node having value Zero is the Non-Last Leaf Node.
Step 2:
Then we have to find out the index of the Left and Right Child of the certain node. To find out the index of the Left and Right Child of the Root Node, we need to go through the formulas. Finding out the index is very important in the array. Depending upon the index we will perform the further operation.
Suppose, the index of the Certain Non-Last Leaf Node is: i. Then,
The formula for finding out the Index of Left Child: 2i+1
The formula for finding out the Index of Left Child: 2i+2
Step 3:
Among the two children, we need to find out which one is greater compared with the Non-Last Leaf Node & in between them also. The largest numbered Node will be swapped with the certain Non-Last Leaf Node.
Here, in this case, the Child Node having value 2 will be swapped with the Non-Last Leaf Node which is zero. This swapping is known as the Heapify.
Step 4:
Now, after successfully swapping, we can build Max Heap with C programming language also. So, it will now create the Max Heap from the previous Heap.
After we build Max Heap time complexity we need to calculate. The programmers build Max Heap time complexity as it is relatively less than others. The time complexity of Max Heap is O(N). The above can be a Max Heap example.
How Much Heap Memory Is Available?
Heapify is one of the most expensive processes in terms of memory consumption. During the checking & reversal of the nodes, the heap consumes some amount of memory from the device. By default, the computer allows 1/64th memory space of the total memory for the heap allocation.
However, the memory allocation is not a static one. The memory space can be increased further using some internal commands which is completely another topic. But in such cases, the heap can utilize the 1/4th memory space of the device without having an issue.
PseudoCode of Heap :
indexOfNode is the root of a subtree
Heapify(array , sizeOfArray , indexOfNode)
Largest = findMaximum of ( indexOfNode , leftChild , rightChild )
If Largest != indexOfNode i.e the root
Swap ( Largest with indexOfNode )
Heapify( array , sizeOfArray , Largest )
How To Make A Max Heap: The Process For Building Max Heap?
If we start making subtree heaps from down to the bottom, eventually the whole tree will become a heap.
The Build Heap function will loop starting from the last non-leaf node to the root node, and call the Heapify function on each. So that each node satisfies the max heap property. Similarly implementing stack in C is easy if you follow the right steps. Have you heard of tree traversal? You can learn this topic as well.
Coming to our topic, we are starting from the last non-leaf node because leaves are already heaps.
To find an index of the Last Non-leaf Node,
index of Last Non Leaf Node = (n/2) – 1
where n is the number of nodes in a tree
-
Supporting Functions
These functions will help with basic utilities for
- Printing an array
- Swapping two variables
-
Driver Code
In general Driver code is written to test your developed program and in the below screenshot, you can find the driver code. If it’s not written well, it might flag an error in the C programming project.
This will run our code.
Final Code Of How To Build Heap From Unsorted Array
We have written the final code for building the max heap. You can refer to this code and practice by yourself. Our codes are very well-commented and written as per college standards.
You can run this code to get the correct output shown below:
// Build a Heap from an Array with C
#include <stdio.h>
// swap function
void swap(int *a, int *b)
{
int temp = *b;
*b = *a;
*a = temp;
}
// Function to print the Heap as array
// will print as - 'message array[]\n'
void printArray(char message[], int arr[], int n)
{
printf("%s ",message);
for (int i = 0; i < n; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
}
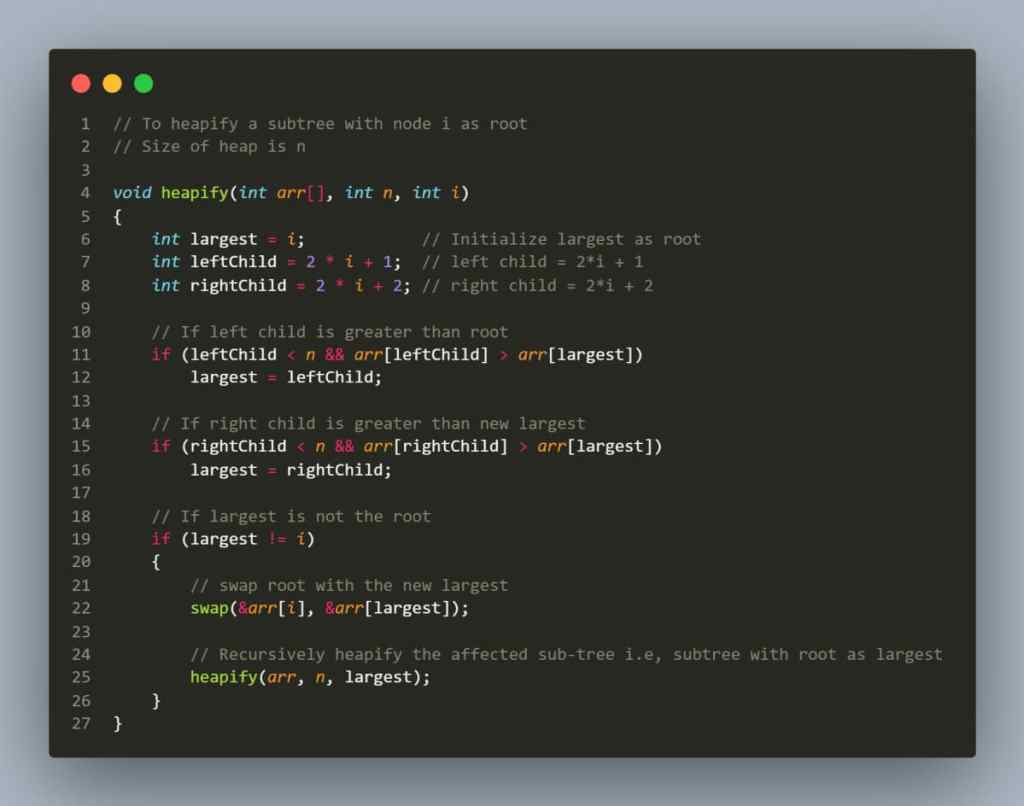
// To heapify a subtree with node i as root
// Size of heap is n
void heapify(int arr[], int n, int i)
{
int largest = i; // Initialize largest as root
int leftChild = 2 * i + 1; // left child = 2*i + 1
int rightChild = 2 * i + 2; // right child = 2*i + 2
// If left child is greater than root
if (leftChild < n && arr[leftChild] > arr[largest])
largest = leftChild;
// If right child is greater than new largest
if (rightChild < n && arr[rightChild] > arr[largest])
largest = rightChild;
// If largest is not the root
if (largest != i)
{
// swap root with the new largest
swap(&arr[i], &arr[largest]);
// Recursively heapify the affected sub-tree i.e, subtree with root as largest
heapify(arr, n, largest);
}
}
// Function to build a Max-Heap from a given array
void buildHeap(int arr[], int n)
{
// Index of last non-leaf node
int lastNonLeafNode = (n / 2) - 1;
// Perform level order traversal in reverse from last non-leaf node to the root node and heapify each node
for (int i = lastNonLeafNode; i >= 0; i--)
{
heapify(arr, n, i);
}
}
// Driver Code
void main()
{
// Array
int arr[] = {4, 18, 17, 10, 19, 20, 14, 8, 3, 12};
// Size of array
int n = sizeof(arr) / sizeof(arr[0]);
printArray("Array is : ", arr, n);
buildHeap(arr, n);
printArray("Array representation of Heap is : ", arr, n);
}
Output:
Input Array :
4
/ \
18 17
/ \ / \
10 19 20 14
/\. /
8 3 12
Output Max Heap :
20
/ \
19 17
/ \ / \
10 18 4 14
/\ /
8 3 12
As we can see every node is greater than its child nodes ( max heap property ). Didn’t understand the code? No issues, You can always ask for programming help from experts at CodingZap.
Time & Space Complexity:
When we are discussing an important Data Structure concept that is also parallelly utilized in the algorithm process, the discussion of Time and Space Complexity becomes inevitable. The Heapify process takes O(logn) time to complete an iteration. The same amount is consumed as Space Complexity.
Now, if we are talking about the Time Complexity of Max Heap where the n terms of the array are inevitable, then it becomes O(n*logn). In that case, the Space Complexity becomes a constant one that is indicated with O(1).
Heap Data Structure Applications:
- Priority queue.
- Dijkstra’s Algorithm
- Heap Sort
Conclusion:
As we saw, knowing how to build Max Heap with C programming language is very important.
We should clear the basics of recursion & function calling to learn how to build Max Heap with C programming language.
We should clear the heapify method. That is very important among all the functions while building Max Heap with C programming language.
So, hope you have liked this piece of article. Share your thoughts in the comments section and let us know if we can improve more. Still, curious about learning C programming then here is the guide to start learning C in 5 easy steps.